A perspective on perspective

Life's an illusion. Surrounded by atoms, radiations and reflections, we use our senses and intelligence to 'make sense of' this jumble and convert it into the imaginary environment we perceive around us. Sight is no exception. The brain has somehow cottoned on to the fact that light travels in straight lines and uses this, amongst other things, to create our 3D world.

The brain judges distance by colour variation and shading, size, overlapping, shape and position. Get these right and you have your imaginary 3D world. We shall just consider perspective.

As objects recede into the background they also appear smaller and closer to each other, and parallel lines appear to converge into the distance at what is known as a vanishing point. This perspective effect was first formulated by Alberti in 1435 (available in Penguin) and we shall be using these principles in this tutorial.

A distortion of the truth. Fellow countryman Leonardo da Vinci pointed out that this wasn't the whole truth; looking head on at a long, parallel beam (a transversal), the ends should appear smaller than the middle since they are further away; the same is true about verticals. We shall ignore this effect as Alberti did and our brains tend to, and keep all straight lines straight, but we'll limit our angle of vision to 60 degrees or so to minimise the distortion which would otherwise occur at the edges of our picture.

Your perspective horizon is at eye level. Every picture has a horizon. The visible horizon will depend on the terrain, but for perspective considerations we should forget this, and mark the viewer's horizon, at eyeball level. As you climb, so does your perspective horizon - up the picture. If you want a worms-eye view your horizon will be lower.
A second significant level is ground, or floor, level, usually the bottom of the picture. Lines parallel to the horizon and ground line are called transversals.

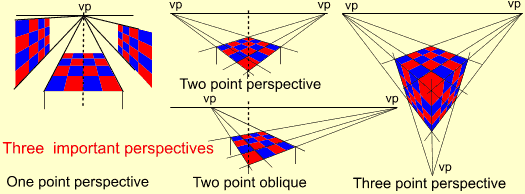
Every point is a vanishing point. For every line direction there is a different vanishing point. Except for transversals, all lines parallel to each other in the real world appear to converge to the same point at infinity. All horizontal parallel lines converge to a point on the horizon. As you face the horizon, every horizontal line parallel to the direction of your vision appears to converge to the same point on the horizon directly in front of you, known as the central vanishing point. If the objects viewed (such as a cube end on) line up with these lines, perspective is simple as it only has one vanishing point. Once you rotate the cube, the vanishing point moves along the horizon and what were previously transversals now converge at a vanishing point that comes in from the other side, giving a two point perspective. If you now tilt your cube upward, then your vanishing points move upwards too and the verticals now converge to a third vanishing point which comes up from below. Fortunately, human constructs tend to be at right-angles, and three points are enough for most pictures. Any four-sided plane can have up to two vanishing points and in the case of the cube you will notice that the six points coincide at three locations.

Cone, angle, or field of vision. If we fix the angle of vision for our picture at, say, 60 degrees, this will effectively define how far from the picture is the view point, often called the station point. If you have a camera with a zoom lens you will know that as you zoom in, the perspective of your photo changes. It becomes more flattened. This is because objects are projected into the vertical plane of the camera, and the amount depends on the angle the object is viewed from, and this brings us neatly to the other aspect of perspective - foreshortening. Now we have established the horizon, floor plane and vision angle we are in prime position to solve the remaining challenge of perspective - foreshortening.

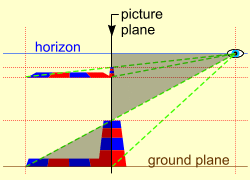Foreshortening. On the left we see two identical chequer boards at different heights viewed from the right, and projected onto the picture plane (as height). Knowing the distance of the eye from the picture, the dimensions of the object and its location it is simple geometry to calculate the projected height on the picture. In fact, if we construct a grid, we can know the foreshortening at any point on the plane.